To appreciate how well a matched filter works in the presence of noise, let us examine the estimation of the delay of an exponentially-decaying signal segment. This exercise builds upon Laboratory Exercise 5.1 and Equation 9.13. The filter is described by:

(9.19)

The signal h[n – 21] is a delayed version of the filter. The noise, N[n], is zero-mean, Gaussian, and independent of the signal. The “corrupted” signal r[n] is given by r[n] = h[n – 21] + N[n].

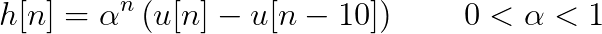
1. Starting from α = 0.9 and SNR = 1000:1, the results in the bottom row appear to differ. Explain why this is so.


2. According to Section 5.1, we should not expect that φ_rh[k] is even. Nevertheless, it appears to be symmetric (even) about its peak value. Explain why this is reasonable. (Note that the peak positions are illustrated in red.)


3. The peak positions of the two computations r[n] ⊗ h[-n] and r[n] ⊗ h[n] are shown. If we hold the SNR constant at 1000:1. which computation—the correlation or the convolution— gives a stable and correct estimate of the delay as we vary the value of α?


4. If we hold the parameter α constant, which computation—the correlation or the convolution—gives a stable and correct estimate of the delay as we vary the value of the SNR? At what value of the SNR do both techniques cease to give a reliable estimate of the delay?


5. Which computation—the correlation or the convolution—gives the best estimate of the delay as we vary the values of both α and the SNR?