We now return to the real, FIR filter used in Laboratory Exercise 6.7a and Laboratory Exercise 6.7b and described as:

(6.48)

The sampling frequency remains 44.1 kHz. The input x[n] is

--

seconds of a white noise signal with a Gaussian amplitude distribution g[n]. The output y[n] = g_F [n] is the filtered version of g[n], that is, g_F [n] = h[n] ⊗ g[n]. As in Laboratory Exercise 6.7b, the frequency-domain technique is used to produce g_F [n] that is:

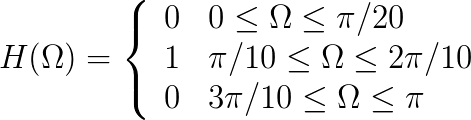
(6.49)

gF [n] = F  –1 {F { h[n] } • F { g[n] }}

where F {•} is the Fourier transform operator. Notice that in the results below the correlation function and the power spectral density are now the cross-correlation function φ_gF(τ = kT) and the cross-power spectral density S_gF(2πf)¹.

1. Why is the cross-power spectral density displayed as |S_gF(2πf)| instead of S_gF(2πf) ?


2. Sketch the impulse response h[n] in as much detail as possible. At what time (in ms), for example, does h[n] have its maximum value?


3. At what time sample (in n) does h[n] have its maximum value?


4. What difference do you expect between S_gF(2πf) and S_FF(2πf) ? (Refer, for example, to Laboratory Exercise 6.7b and to material in this chapter starting at Equation 6.20.)


5. Which of the signals { h_i [n] | i=1,2,3,4 }, shown in the bottom row of this section, could be the impulse response h[n] used in this laboratory exercise?

What does it mean? Understanding the formal relationship between correlation functions, power spectral densities, and linear time-invariant (LTI) filters gives us the tools to understand how ergodic signals will be affected by filtering. Further, given the input and output signals—particularly when the input signal is white noise—allows us to characterize the LTI filter.

¹Each of the signals and correlation functions contains far more samples than can be displayed across the screen of your device. The data are therefore “binned” to fit on the screen. Slight distortions—artefacts of the binning process—are therefore possible. ↵