Laboratory Exercise 6.7a
In this exercise we consider a real, finite impulse-response (FIR) filter h[n] that has been designed to meet the following specifications:
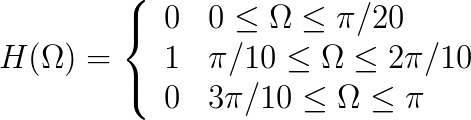
(6.43) Missing Filter specification
  1. What type of filter is this? Explain your reasoning.

  2. When you listen to each of the signals, does this support your answer to the previous question?

  3. If the sampling frequency is 44.1 kHz, what are the corresponding frequencies (in kHz) of the various frequency bands? Explain your reasoning.
The input x[n] is -- seconds of a white noise signal with a Gaussian amplitude distribution g[n]. The output y[n] = gF [n] is the filtered version of g[n], that is, gF [n] = h[n] ⊗ g[n]. The technique used to produce gF [n] is the literal, time-domain convolution of h[n] with g[n].
  1. Do the frequencies where the passband changes to stopband (and vice versa) correspond to the frequencies you expected?

  2. Why is the width of the probability distribution associated with the amplitudes of gF [n] smaller than the width associated with g[n]?
Proceeed to another part of this exercise by choosing the variant below.


Choose lab variant:       → → →

Choose display:         

Zoom: N = ----- samples
= ----- ms

  Play signal g(t)      

  Play signal gF (t)