The application of Equation 10.29—repeated below— requires a lot of prior knowledge.

(10.36)

We need to know H₀(Ω), S_xx(Ω), and S_nn(Ω). There are ways to measure the transfer function of the distortion filter H₀(Ω). But what about the power spectral densities of the signal and the noise?

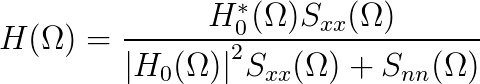
In this exercise we suggest a “poor man’s Wiener filter”. It is based upon a rewritten form of the Wiener filter Equation 10.30 that is given below.

(10.37)

We have frequently assumed that the noise process is white noise, that the power spectral density is flat. This means that S_nn(Ω) = K_nn. This is only a small leap of faith.

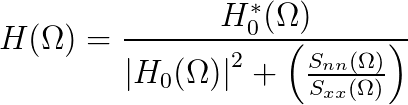
1. What physical constraint stands in the way of this assumption being valid in our real, physical world?

Let us now take a much bigger leap. Let us assume that as we do not know the actual signal—if we did why would we try to restore it?—the power spectral density of the signal is also flat, S_xx(Ω) = K_xx. Our ignorance of the actual form of S_xx(Ω) gives us no basis to assume that any particular frequency band is greater than any other. This means that the “poor man’s Wiener filter”, H_pm(Ω), is given by:

(10.38)

We have replaced the ratio of two constants K_nn/K_xx with the single constant K. The only thing that is now missing is the value of K.

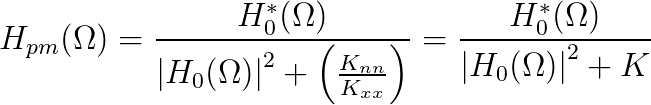
In the experiments below, choose the radius of the aperture (starting from the smallest), different levels of additive, independent, Gaussian noise, and different values of K. As before, the magnitude of the spectrum of the aperture filter will be displayed as well as the SNR and you can rotate the display of the spectrum.

2. At the highest value of the SNR and the smallest radius, what range of values for K leads to restorations that are comparable to the original.


3. Now change the SNR to 10:1 and adjust K to produce (in your estimation) the best possible restoration. Which version resembles the original version most: the noisy and distorted version (lower, left panel) or the restored version you have produced by adjusting K (lower, right panel)?


4. Repeat the previous experiment while systematically decreasing the SNR from its highest value and looking for the value of K that yields the best restoration. As the SNR decreases which version resembles the original version most: the noisy and distorted version (lower, left panel) or the restored version (lower, right panel)?


5. Does there seem to be a relationship between the choice of K and the SNR? Is there an explanation possible based upon the above equation?

Now repeat the above experiments for various values of the aperture radius.

6. For each aperture size, at what SNR is the filter not useful in restoring the image? You might also consider making a distinction between “recognizing an image” and “restoring an image”.