Consider yet another real, stable, discrete-time, LTI system whose input/output relation is given by:

(6.40)

where x[n] is the input and y[n] is the output. The impulse response is h[n] and its Fourier transform is H(Ω).

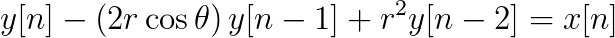
The input to this system is x[n] = g[n], a

1.5

second white noise signal with a Gaussian amplitude distribution. The output is y[n] = g_F [n] the filtered version of g[n], that is, g_F [n] = h[n] ⊗ g[n].

1. What is the z-transform H(z) of the impulse response h[n]? What is the associated region-of-convergence (ROC) of this z-transform?


2. Is the stochastic signal g_F[n] a “white” noise signal? Explain your reasoning.


3. Based upon the data presented, what type of filter is h[n]: a lowpass filter, a highpass filter, a bandpass filter, or a band-reject filter?


4. When you listen to each of the signals, does this support your answer to the previous question?


5. Both g[n] and g_F [n] have been normalized after analysis but before being converted to audio WAV files. Do they sound equally loud? If not, can you think of an explanation? (Full disclosure: They do not sound equally loud to this author.)


6. At what (approximate) frequency (in kHz) does this filter have its maximum amplitude? What is the corresponding value of θ in Equation 6.40? Why is the term “approximate” used in this question? (Hint: It might help to make a pole-zero plot of H(z).)


7. Describe the relationship between the autocorrelation function φ_FF(τ = kT) and the impulse response h[n].

Proceeed to another part of this exercise by choosing the variant below.