The purpose of this exercise is to review the methodology for computing the Fourier transform of a discrete-time signal based upon a given set of data x[n] with n = 0, 1, ..., N–1. This is frequently referred to as the DFT (Discrete Fourier Transform) and is defined by Oppenheim¹:

(12.25)

It is important to note that X[k] = X(Ω_k)/N if the signal is identically zero outside the interval 0 ≤ n ≤ N–1. The DFT is then a version of F {x[n]} that is harmonically-sampled (Ω_k = kΩ₀ with Ω₀ = 2π/N) and scaled (by 1/N).

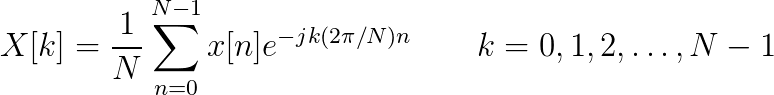
1. Consider the continuous-time signal x(t) = sin(2πf₀t). What is the Fourier transform X(ω) of this signal?


2. Now consider the discrete-time signal x[n] = sin(Ω₀n) What is the Fourier transform X(Ω) of this signal?

In the following experiments we work with a sampled sinusoidal signal with a variable frequency f₀ and variable phase φ. The signal x[n], depending upon the number of samples shown, is displayed as a smooth curve or as discrete samples. The power spectral density spectrum S_xx(Ω) based on the DFT spectrum X[k] is indicated by vertical bars for the various values of k. To make the connection between k and continuous-time frequency, the horizontal axis is labeled in units of Hz (f = ω/2π) instead of Ω, a concept used in previous chapters as well. At any time you can listen to a signal using the () button.

The signal is sampled at a rate of

44.1

kHz and consists of

3700

samples. From these samples, a window of N samples is displayed.

3. Does the power spectral density S_xx(ω) corresponding to the frequency f₀ match your expectations? Explain.


4. Does changing the “zoom” change S_xx(ω)?


5. Does changing the phase φ change the S_xx(ω)? Explain.


6. If you choose another frequency f₁ ≠ f₀, does the new power spectral density differ from the original S_xx(ω)? If so, in what ways does it change?


7. Are there other frequencies, f₁ ≠ f₀, for which the power spectral density appears to be a purely shifted version of the original S_xx(ω)?


8. Explain why the power spectral density S_xx(ω) for some values of f is a shifted version of the original S_xx(ω) and for some values of f it is not.

¹Oppenheim, A. V., A. S. Willsky and S. H. Nawab (1996). Signals and Systems. Upper Saddle River, New Jersey, Prentice-Hall  ↵